В рамках интерактивного занятия ребята изучили парадокс Аристотеля о вращающихся колесах, разминали свои умы и расширяли свои горизонты.
Мы убеждены, что вовлечение детей в изучение наук уже с самого детства является ключом к развитию их критического мышления и творческих способностей.
Наша цель — вдохновить будущее поколение на увлекательные исследования и открытия!
Впервые данный парадокс был описан еще в глубокой древности в книге «Механика». Создателем задачи считается Аристотель, хотя сегодня некоторые исследователи этот факт оспаривают. Впрочем, это не так уж важно. Куда интереснее, что над парадоксом колес Аристотеля ломало головы не одно поколение механиков и математиков. В их числе были такие известные ученые умы, как Галилео Галилей, Рене Декарт и Пьер де Фема. Впервые парадокс Аристотеля был правильно разгадан лишь в 1715 году.
В чем заключается парадокс колес Аристотеля?
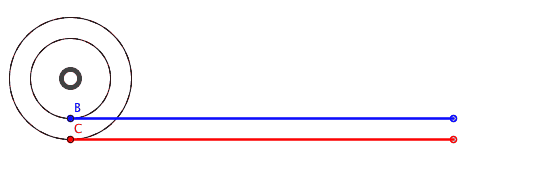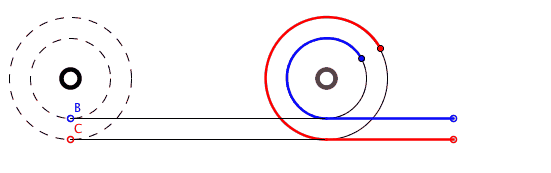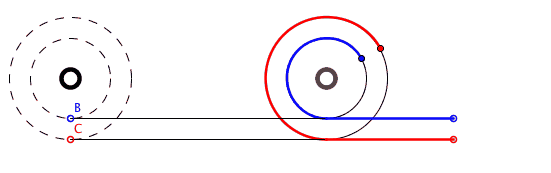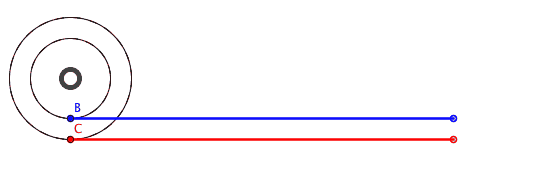
Как должно быть в теории при 1 полном обороте.
Парадокс колес Аристотеля заключается в том, что два совмещенных колеса с разными диаметром проходят без проскальзывания путь равный длине окружности большего колеса. При этом внутреннее колесо меньшего размера по какой-то причине проходит тот же путь за аналогичное количество оборотов, чего в теории быть не может. Парадокс Аристотеля заключается в том, что математические расчеты в данной задаче не совпадают с действием физической модели.
На самом деле задача Аристотеля достаточно «жульническая», и весь подвох парадокса заключается в несовпадении физической и математической модели. Дело в том, что если построить физическую модель совмещенных колес Аристотеля, то окажется, что одна из окружностей при прохождении пути просто проскальзывает. Собственно, ошибка, порождающая парадокс, в том и заключается, что решающий задачу выдвигает неправильное предположение о том, будто бы внутреннее (меньшее) колесо подобно внешнему (большему) движется без проскальзывания.
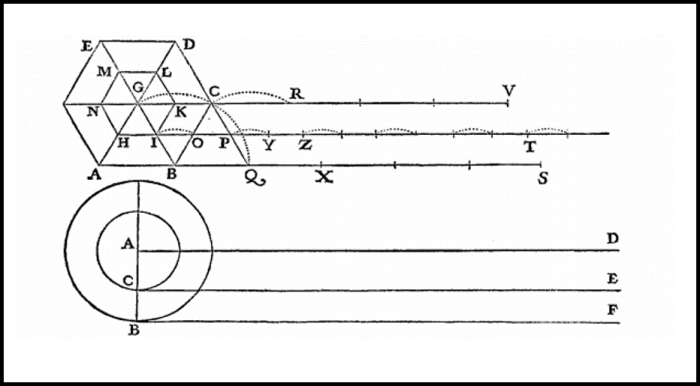
Проскальзывание становится очевидно, если заменить круги на другие фигуры.
Причем данный парадокс одинаково работает для обеих совмещенных окружностей. Так, если заставить конструкцию вращаться не по большему, а по меньшему радиусу, то проскальзывать будет уже не меньшая окружность вслед за большей, а большая вслед за меньшей. Кстати, каждый может сам проверить действие парадокса, просто покрутив в руках бутылку и понаблюдав за горлышком и дном сосуда.